从音类集合到集合类

• 以特里斯坦和弦 $\{F,B, \sharp D, \sharp G \}$ 为标志，瓦格纳突破了传统和弦的调性功能，强调和弦本身的声音效果和色彩，进而消解了调式音阶对于和弦使用的束缚。
• 勋伯格《钢琴组曲》中《加沃特组曲》就包含音类 $\{\flat D,E,F,G\}$
• 音类集合：由若干音类构成的集合，简称pc集。
• 包含 $n$ 个音类的pc集称为 n元pc集，因为音类空间只有12个音类，因此 $0 \leq n \leq 12$ ，任意pc集都可以看成音类空间的子集合。
• 根据对应关系，也可以将pc集对应于模12集合的子集。
• 音类集合中元素是音类，不是构成传统和弦的音级，元素无须满足三度叠置原则。
• 从音类集合角度看，音阶也是pc集。
• $5$ 元pc集 $\{\sharp F,\sharp G,\sharp A,\sharp C,\sharp D \}$ 对应于五声音阶。
• $6$ 元pc集 $\{C,D,E,\sharp F,\sharp G,\sharp A\}$ 对应于全音音阶。
• $12$ 元pc集 $\{C,\sharp C,D,\sharp D,E,F,\sharp F,G,\sharp G,A,\sharp A,B\}$ 对应于半音音阶。
• 一个 $n$ 元pc集可以表示为音类圆周上的内接 $n$ 边形。
• 对于任意两个音类，定义它们之间距离为音类圆周上从 $X$ 出发，到达 $Y$ 经过的最少音类数。
• 对于任意两个不同音类， $1 \leq d \leq 6$ 。
• 一个 $n$ 元pc集，作为一个 $n$ 边形，顶点连线分别构成其边和对角线。
• 定义其距离向量 $\delta=(d_1,d_2,\ldots,d_6),d_i$ 表示距离为 $i$ 的顶点数目。
• 距离向量给出了一个pc集中所有音类对之间的距离，描述了其全部音程含量，在很大程度上刻画了该pc集对应的乐音组合的声音效果。
• 总结一下，目前达到了音级->音类->音类集合的抽象层次。
• pc集是无序集合，为了便于比较和识别不同pc集，根据紧凑原则对每个pc集规定一个标准表达式，称为其标准序或者标准形。
• 由组合恒等式可以推出，一共有 $2^{12}=4096$ 个pc集。
• 同时，由 $220$ 个三元pc集。
• 如果一个pc集经过某些音乐上的变换得到另一个pc集，那么这两个pc集在音效、色彩等方面会具有一定相似性。
• 移调变换可以作用在音类集合上，对于某个pc集作移调变换，可以得到12个pc集，对应12个大三和弦。
• 即，对于任意两个大三和弦，总可以找到某个移调变换使其相等。
• 也就是，12个大三和弦属于同一条轨道，可以把其归为同一个类。
• 倒影变换也可以作用在音类集合上，它把大三和弦变为小三和弦。
• 同时 $T * I$ 把大三和弦变为另一个小三和弦。
• 进而， $T^{i} * I$ 变换可以把 $\{C,E,G\}$ 变成某个与小三和弦对应的pc集。
• 任意给定两个大三和弦或小三和弦，必存在群中变换使其相等，从而24个大小三和弦属于同一条轨道，归为同一个类。
• 举一个具体例子：

• 在群 $\langle T,I \rangle$ 的作用下,pc即按照其轨道被分为若干等价类，一个pc集的等价类被称为一个集合类。
• 例如，220个3元pc集被分为12个等价类，形成12个集合类，其中24大小三和弦对应的pc集属于同一个等价类/轨道。
• 按照一定方法在每个集合类中取一个pc集作为代表，得到音类集合表，集合类代表的标准序称为这个集合类的原型。
• 艾伦-福特给每个集合类起了一个名字，k-x， $k$ 是pc集代表的音类数目， $x$ 是序号。
• 例如，增减三和弦对应的音类集合为 $3-12$ 和 $3-10$ 。
• 同时，减七和弦对应的音类集合为 $4-28$ 。
• 另外，属七和弦和半减七和弦对应的音类集合为 $4-27$ 。
• 全音程和弦：距离向量为 $(1,1,1,1,1,1)$ ，一共有 $4$ 个音类。
• 例如， $\{B,C,D,\sharp F\},\{C,\sharp C,E,\sharp F\}$ 都是全音程和弦。
• 全音程和弦构成不满足三度叠置原则，它不是传统七和弦。
• 在调性音乐中，只有极特殊的情况才会出现，但是在无调性音乐中，全音程和弦有重要地位。
• 定理：在群 $\langle T,I \rangle$ 作用下，只有两类互不等价的全音程和弦， 即 $4-Z29$ 和 $4-Z15$ ，如下

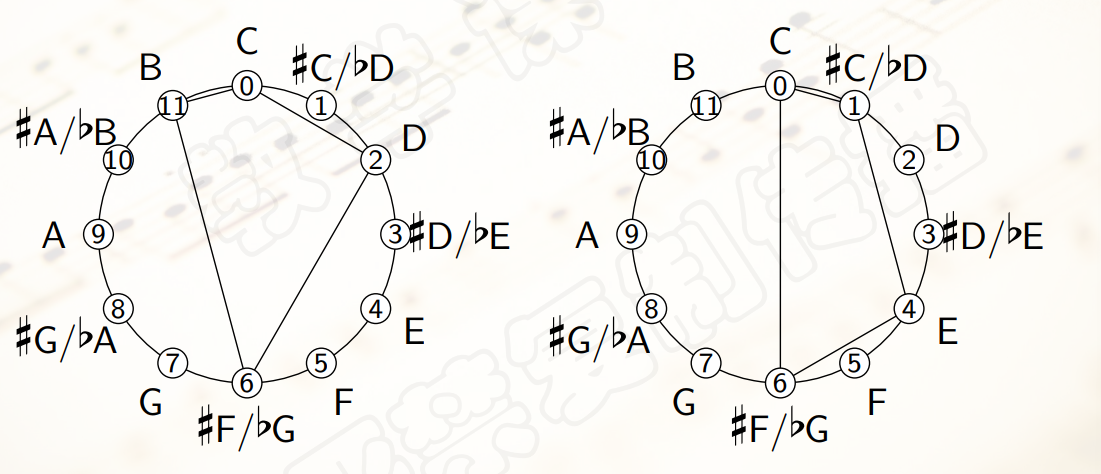
• 定理：移调变换和倒影变换不改变pc集的距离向量，从而同一个集合类中的pc集具有相同距离向量。
• 但是，具有相同距离向量的两个pc集可能分属不同集合类，例如两种全音程和弦。
• 于是，构成音级->音类->音类集合->集合类的抽象层次。
• 在任何一个特定的音乐语境中，只有少数子集合具有音乐上的意义。
• 如果pc集 $A$ 的音类都包含在pc集 $B$ 中，称其为字面上子集合；若 $A$ 在某个变换下的像是 $B$ 子集合，称其为抽象的子集合。

和弦连接与黎曼变换

• 协和三和弦，由24个大小三和弦对应的pc集构成的集合类，其为 $3-11$ ，距离向量 $\delta=(0,0,1,1,1,0)$
• 为了简化符号，省略表示等价类的上划线记号，大写 $X$ 表示以 $X$ 为根音的大三和弦，小写 $x$ 表示以 $x$ 为根音的小三和弦。
• 具有相同根音的大小三和弦称为平行的大小三和弦。
• 定义平行变换 $P$ ，把任意一个三和弦变成与之平行的三和弦，它把小三和弦的三音升高半音，把大三和弦的三音降低半音。
• 称大三和弦 $C$ 和小三和弦 $a$ 是关系三和弦，大三和弦 $\sharp F / \flat G$ 和小三和弦 $\sharp d / \flat e$ 也是关系三和弦。
• 定义关系变换 $R$ ，把任意一个三和弦变成其关系三和弦。
• 导音变换 $L$ ：把大三和弦的根音降低一个半音，把小三和弦的冠音升高一个半音。
• 这三个变换统称为黎曼变换。
• 以下是它们的几何解释：

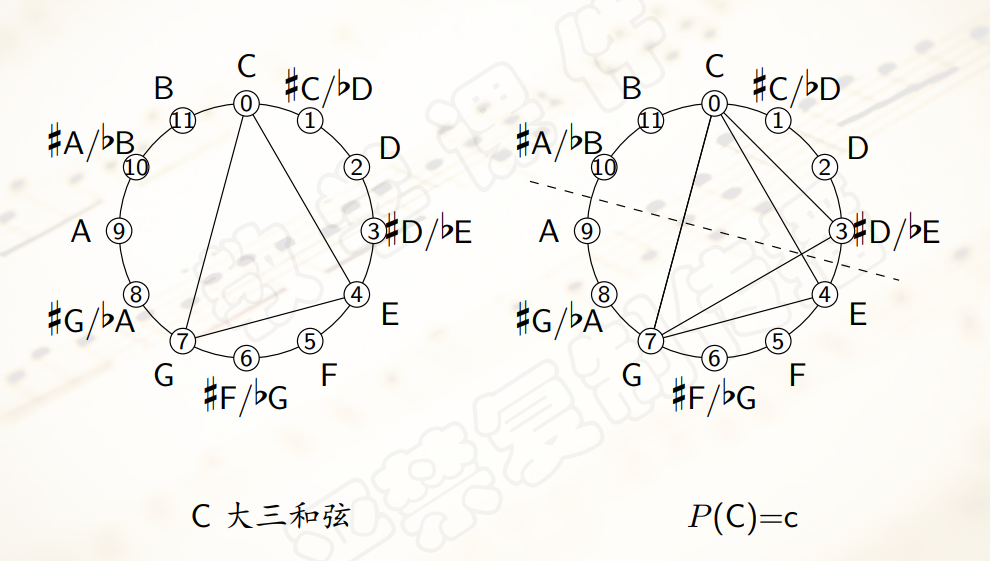
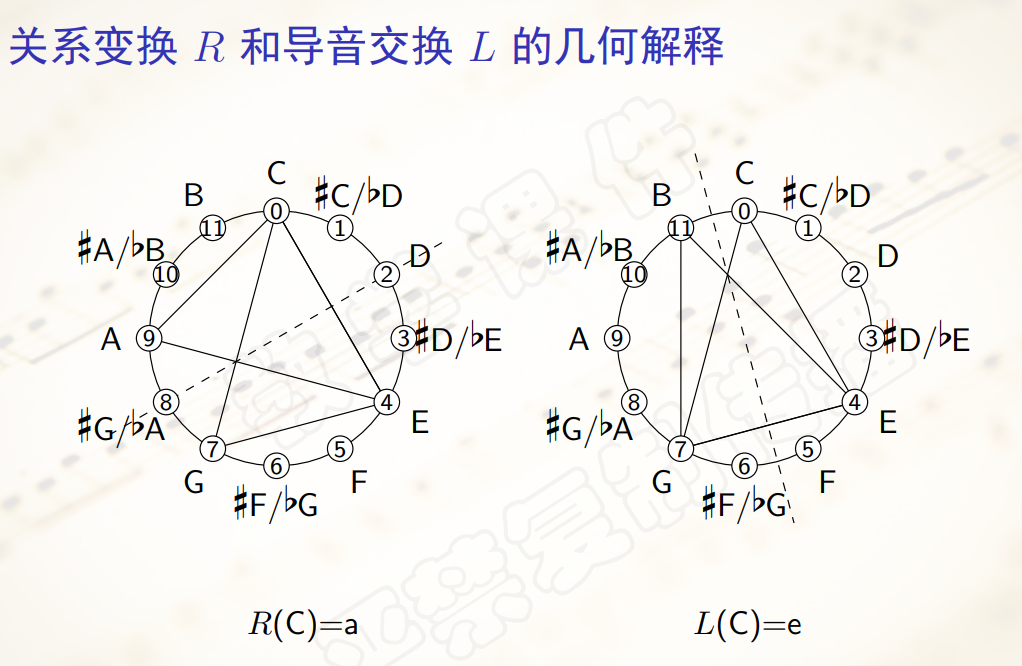
• 从几何上看，这三个对称都只改变三角形的一个顶点，保持另外两个顶点不动。
• 从音乐上看，这三个变换都只改变三和弦中的一个音类，保持其他两个音类不变，从而变换前后的和弦共享一个音程。
• 平行变换只改变和弦的三音，保持纯五度音程不变。
• 关系变换保持大三度音程不变。
• 导音变换保持小三度音程不变。
• 《贝多芬第九交响曲第二乐章》即是很好的实例。

音网

• 欧拉最早意识到声音不只是线性的，可以在二维上拓展形成音网。
• 从大三和弦 $C$ 出发，用 $P,R,L$ 依次作用，可以得到一个循环。
• 从大三和弦 $E$ 出发也是相同的。
• 以任意一个音类为根音，可以构造一个大三和弦，一共有12个大三和弦，从任意一个大三和弦出发，构造 $P,R,L$ 循环，可以得到12个互不相同的循环，对应12个正六边形。
• 将这些正六边形按照其公共边重合起来，得到一个网状的图，称为音网。

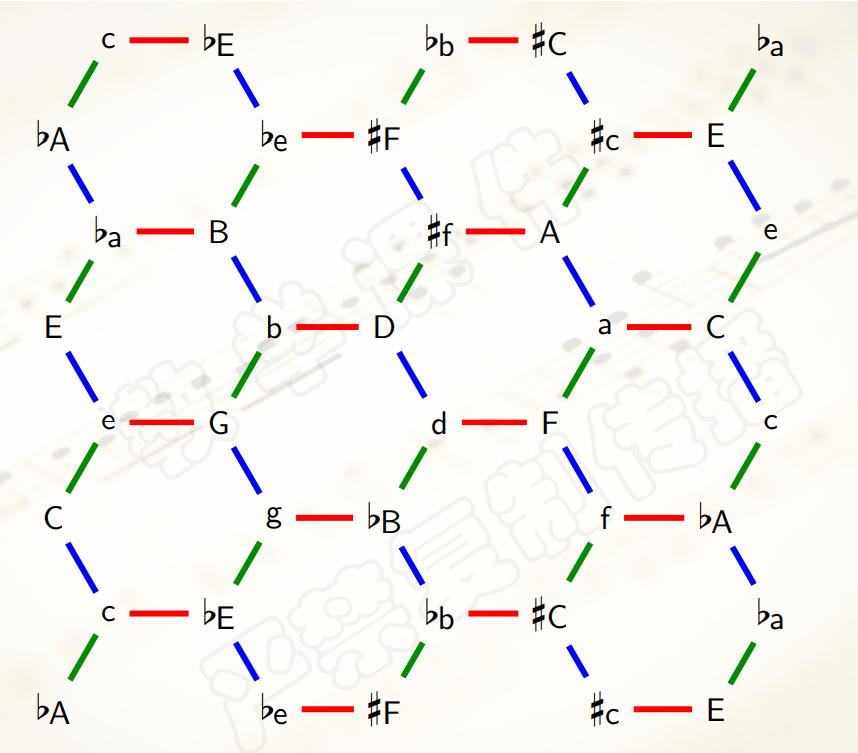
• 用正六边形对应的6个三和弦共同包含的这个唯一的音类作为这个六边形的标号，于是把音网表示为若干带标号的正六边形构成的图形。

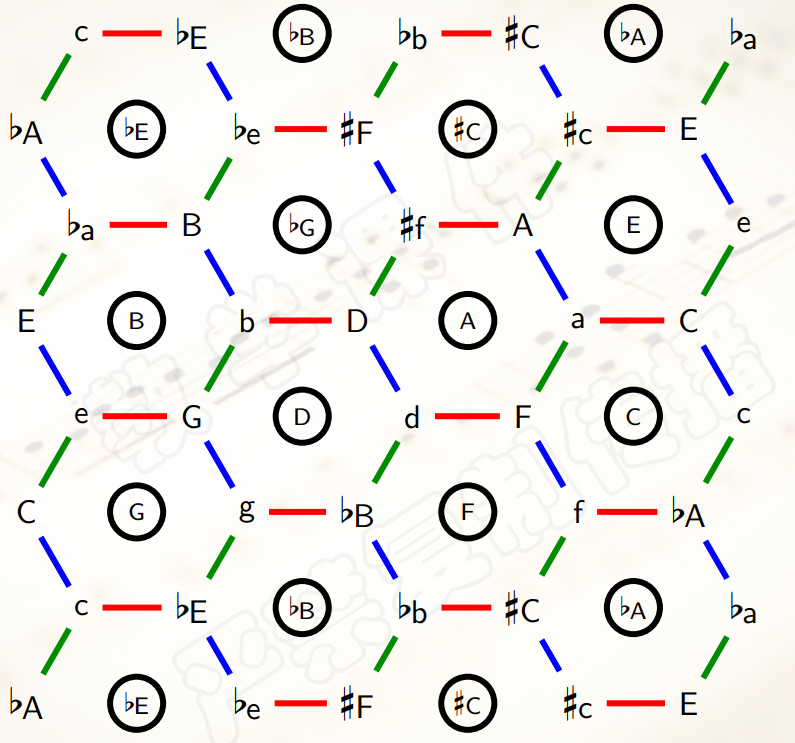
• 同时，音网中两个六边形是否相邻，在某种程度上反映了这两个六边形的标号所构成的音程是否协和。
• 然后，由于每个六边形都有标号，把它们连起来，可以得到音网的对偶图。

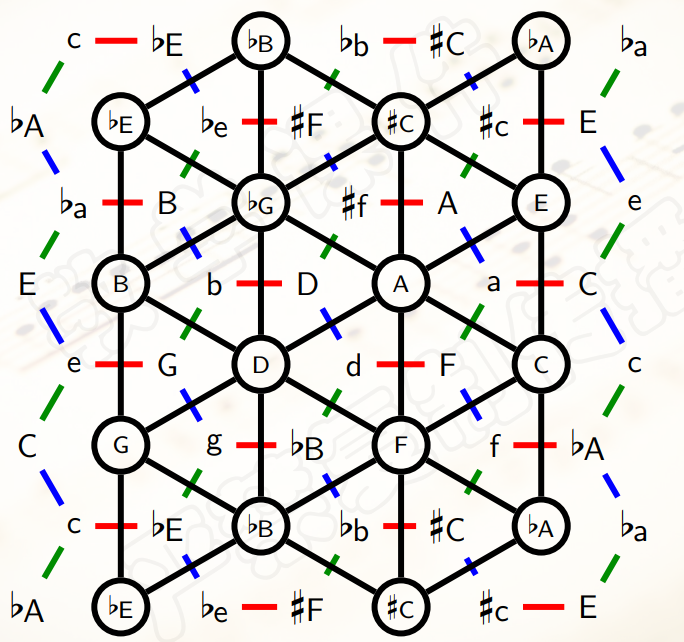
• 进而可以得到对偶音网中三角形的表示形式：

• 在十二平均律体系内，音网实际上并不是无限延展的，而是在水平和垂直两个方向出现周期性的重复。在几何上，这样的一个具有双周期的图形构成一个环面。
• 下面是和弦在音网上的表示：

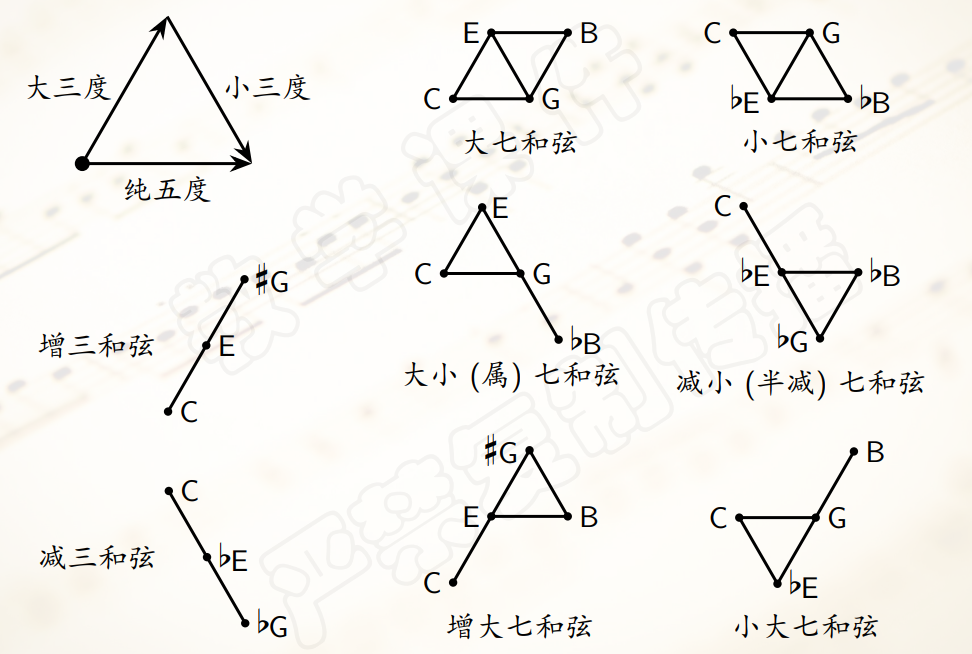
• 同时，音网上还可以找出音阶：

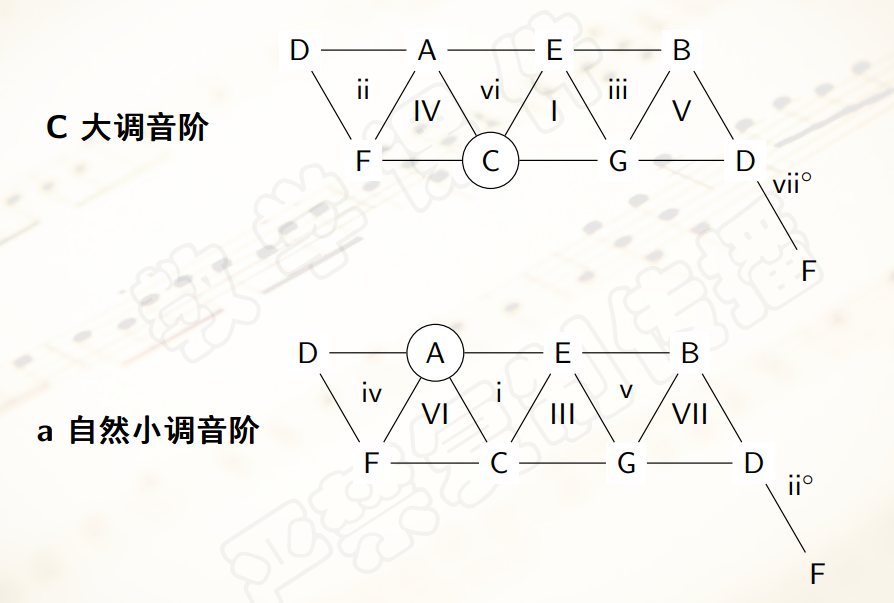
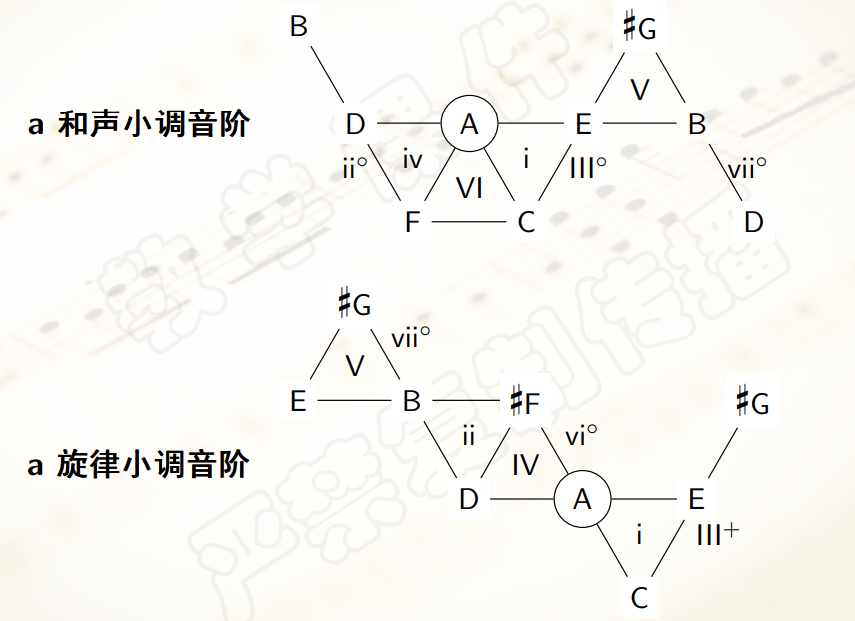
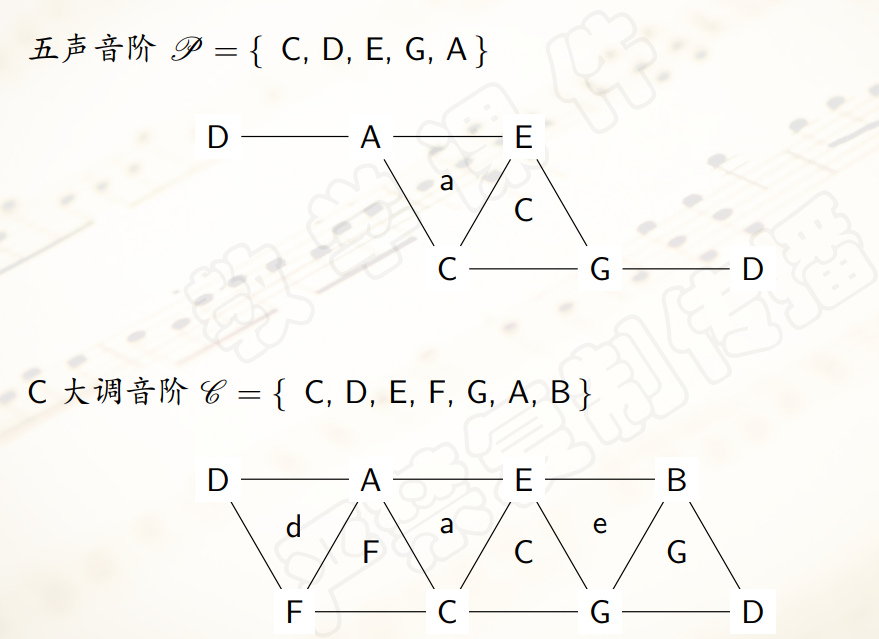
• 钢琴曲《梦》就很完美地体现了这一点。

新黎曼群

• 黎曼三变换仍然建立在调性音乐的理论基础上，后来的音乐理论家将这三个变换纳入音乐变换理论框架，形成了新黎曼理论。
• 大小三和弦集合上的三变换形成了一个群，称为新黎曼群。
• 其同构于 $24$ 阶二面体群 $D_{24}$ 。
• 同时， $R$ 和 $L$ 可以生成 $P$ 。
• 新黎曼群的变换涵盖了传统的和声进行。
• 设 $G$ 是一个群， 子集合 $S \subset G$ 是 $G$ 的一个生成元集合， $S$ 上的一个字是一个形如 $s_1^{\epsilon_1} * s_2^{\epsilon_2} \ldots s_k^{\epsilon_k}$ 的表达式，其中 $s_i \in S,\epsilon_i = \pm 1,1 \leq i \leq k$
• 在新黎曼群中， $S=\{P,R,L\}$ 是一个生成元集合， $R * P * R * L * R$ 等都是 $S$ 上的字。
• 给定新黎曼群中一个字，从音网中某个三和弦出发，用这个字中的变换依次作用到三和弦上，得到三和弦的一个序列，在音网上相应地形成一条从这个三和弦出发的路径。
• 新黎曼群中的元素 $L*R$ 是 $12$ 阶的。
• 因此上述和弦序列可以继续延长，直到遍历 $24$ 个大小三和弦后最终回到出发点 $C$ 。
• 由此也可以推出 $\langle L,R \rangle$ 同构于 $D_{24}$
• 环面上的音网图包含一个哈密顿回路，说明可以从一个三和弦出发，通过一系列变换，使得 $24$ 个大小三和弦每个都恰好出现一次，由于每个新黎曼变换都只把三和弦中的某一个音级变换半音，因此可以平滑遍历全部大小三和弦。