随机作曲

• 1757年，克恩伯格提出了音乐骰子游戏。
• 即预先准备好一系列音乐片段，演奏时通过掷骰子确定使用哪个片段。
• 片段经过精心设计，可以顺畅衔接。
• 以小步舞曲为例，通常采用 $A \rightarrow B \rightarrow A$ 的曲式，每个部分包含8个小节，每个小节有6种可能性，那么一共有 $6^{16}$ 种不同乐曲。
• 随机变量和概率分布的概念，在《高中数学选择性必修三》和《信息学中的概率统计》课程中均有涉及，此处不再赘述。
• Illiac组曲是美国作曲家和化学家借助Illiac计算机完成的弦乐四重奏，采用了包含两个半八度、31个音级的集合，计算机产生均匀分布的随机数完成创作。

马尔科夫链

• 可以把音乐看成是一个随机过程。
• 假设 ${\xi_t }$ 是一个离散随机变量的序列，每个随机变量都有相同的取值范围 $\Omega$ ，这个随机变量的序列构成一个随机过程。
• 将 $\Omega$ 称为 $\xi_t$ 的状态空间。
• 条件概率的概念也有涉及，不再赘述。
• 设 ${\xi_t }$ 是一个随机过程， $\Omega$ 是一个状态空间。若 $\forall n \in N^{+}$ 和 $n+2$ 个状态 $k_0,k_1,\ldots,k_n,k_{n+1} \in \Omega$ ，条件概率总满足下述关系 $P(\xi_{n+1}=k_{n+1}| \xi_0=k_0,\ldots,\xi_n=k_n)=P(\xi_{n+1}=k_{n+1} | \xi_n=k_n)$
• 就称这个随机过程具有马尔科夫性质，具有马尔科夫性质的随机过程称为马尔科夫链。
• 也称为无记忆性。
• 一个马尔科夫链称为时间齐次的，若 $\forall x,y \in \Omega,$ 相应的条件概率不随时间变化，即 $\forall t>0,P(\xi_{t+1}=y | \xi_t=x)=P(\xi_{t}=y | \xi_{t-1}=x)$
• 此时可以使用一个矩阵刻画其行为。
• 设状态空间 $\Omega$ 包含 $n$ 个元素， $\forall k_i,k_j \in \Omega$ ，记条件概率 $P(\xi_{t+1}=k_j|\xi_t=k_i)=p_{ij}$ ，则其为状态 $\xi_t=k_i$ 到 $\xi_{t+1}=k_j$ 的转移概率，并且形成这个马尔科夫链的转移概率矩阵。
• 转移概率矩阵的每一行元素之和都等于1，给定当前状态，就能知道下一个状态的概率分布，即第 $i$ 行。
• 也就是给定 $\Omega$ 和 $P$ ，从 $\xi_0=k_0$ 出发，可以根据下一个概率分布随机选定，于是循环往复，就可以得到一段随机旋律了。
• 例如，在《鸿雁》中，总共出现 $8$ 个音级，假定只考虑音高，不区分相同音高但是时值不同的音符，就可以得到状态空间了。
• 高阶马尔科夫链，就是一个状态只与过去的 $m$ 个状态有关，称相应的随机过程是一个 $m$ 阶的马尔科夫链。

遗传算法

• 遗传算法是模拟生物中的遗传、变异和自然选择过程的一种搜索全局最优解的方法。
• 出发点是由若干个体组成的种群，例如由若干乐曲片段组成的种群。
• 遗传算法要对这些个体进行交叉、变异等操作，使它们进化产生下一代种群。
• 根据音乐本身的性质要求事先设定适应度函数，用以衡量进化结果。
• 不断迭代，直到产生需要的进化结果或者达到预设的迭代次数。
• 音级：假定需要考虑的乐音体系包括 $n$ 个音级，分别用 $1,2,\ldots,n$ 表示，用 $0$ 表示休止符。
• 时值：假定乐曲中时值最短的是十六分音符，则每一个音级编号代表一个十六分音符。
• 延长记号：用 $n+1$ 代表延长一个十六分音符的时值。
• 假设每一个个体由两小节构成，交叉即交换两个个体的基因片段，产生两个新的个体。
• 变异即随机改变一个个体的某一点基因，产生一个新的个体。
• 复制，事先给定一个阈值，适应度高于该阈值的个体直接进入下一代。
• 针对作曲的特殊变异：移调、倒影、逆行
• 进化操作中交叉和变异各自所占比例预先给定。
• 适应度函数：对于每一个可能个体 $i$ ，定义一个评判其"好坏"的值，算法根据每个个体的适应度来选取产生下一代的亲本。
• 产生适应度函数：
  • 根据音乐本身规律，如协和。
  • 根据统计结果给出各项的理想数值。
  • 人机交互
  • 机器学习
• 个体选取：轮盘赌算法
• 设当前种群共有 $N$ 个个体 $i_1,i_2,\ldots,i_N,1 \leq k \leq N$ ，则个体 $i_l$ 被选取称为亲本的概率为 $\frac{f(i_l)}{\sum\limits_{i=1}^{k} f(i_k)}$
• 给定种群中个体数目 $N$ ，适应度阈值 $\alpha$ 和迭代次数 $M$ ，随机生成初始种群，使用以下算法迭代。

音乐信息检索

• 音乐信息检索/MIR
• 音乐流派分类，可以使用人工智能技术自动识别，即机器学习。
• 机器学习的概念，此处不予赘述。

• 编码就是压缩和降维的过程。
• 监督学习
  • 回归分析
  • 神经网络
  • 支持向量机
• 无监督学习
  • 聚类分析
  • 关联分析
• 通常将学习样本分为两部分，训练集和测试集，有时候还要选出一部分作为验证集。

生成式人工智能

• 生成式人工智能的任务是通过学习真实世界中对象，进而可以产生出新的对象，也就是具备泛化能力。
• 自然语言、图像、音乐等具有一定随机性，但也有很强的规律性，符合某个未知的概率分布。
• 其任务是通过学习观察到的样本，建立其真实世界中特定对象概率分布的近似模型，接着从这个近似的概率分布中产生新样本，也就是创作。
• 在一幅有意义的图像或者画作中，像素值是由一定关联和约束的，但是无法清晰、明确地描述，也就是隐性知识，否则完全随机的可能是一幅噪声图像。
• 例如，可以把一段音乐编码为高维空间中的一个点。
• 可以使用Diffusion模型，也就是不断去除噪声。
• 每个噪声预测器，预测出哪些是噪声，加以去除。
• 正向的过程是，用完整图像一步步加上噪声。
• 然后再用这个形式训练噪声预测器，就形成Diffusion模型。
• 也可以使用生成对抗网络，即GAN，它的原理大致如下：

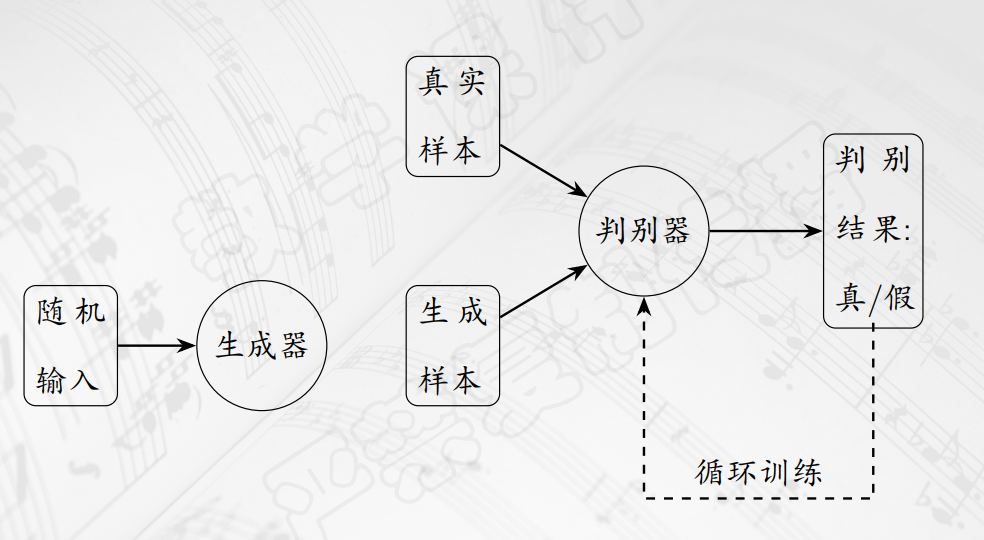
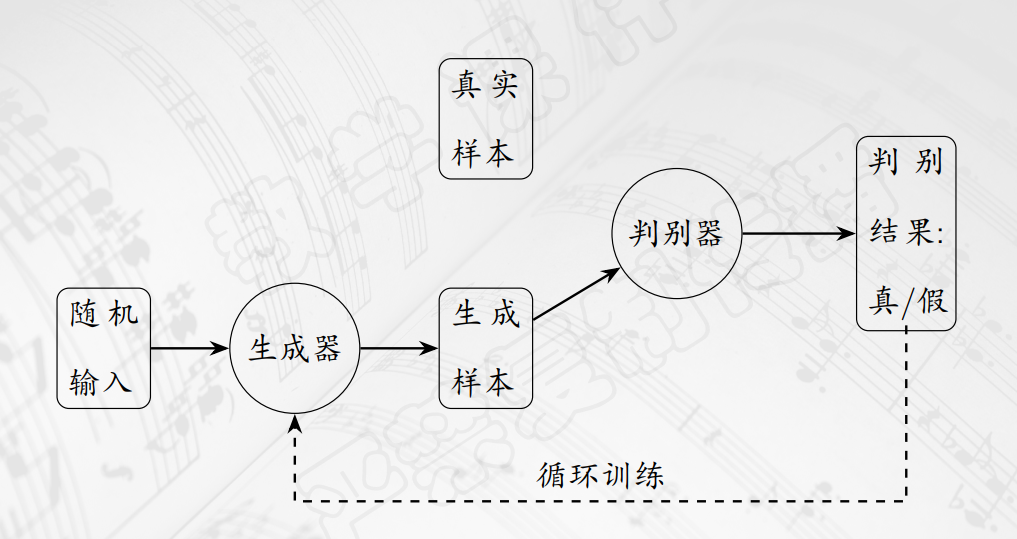
• Transformer模型：传统RNN难以捕捉长距离依赖关系，且难并行化。
• 其核心为自注意力机制，为输入序列中每个位置分配一个权重，然后将这些加权的位置向量作为输出。
• 注意力权重的计算涉及向量的点乘和矩阵乘法，其中权重通过训练得出，对于每个token都可以单独进行，向量和矩阵运算可以由GPU并行完成。