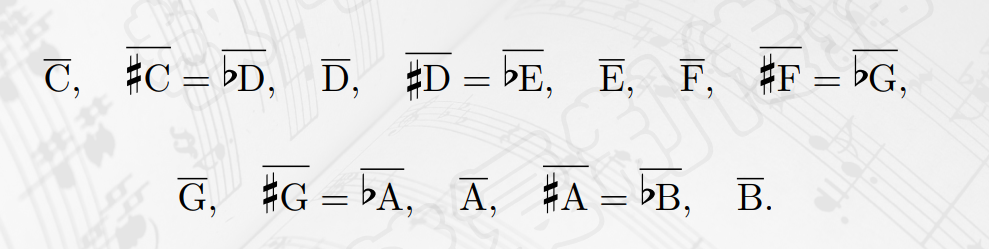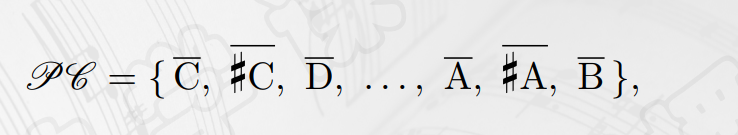旋律与对称

旋律中的对称、群论

许多不同音高、不同时值的音符组合起来构成旋律，是音乐三大要素之一。
重复原则是音乐发展的一项特殊美学原则。
旋律在一次次重复中不断变化、发展。
变化旋律最简单的方法是移动它们的音高，即移调。
贝多芬 $c$ 小调第五交响曲第一乐章开始的"命运"主题，第三四小节相比第一二小节降低了二度移调。
南泥湾也是，15、16小节把前两个小节旋律严格降低一个纯五度。
严格移调：把一段旋律中每个音级升高或者降低相同半音数。
调性移调：适当调整升高或降低的半音数，使得移调后得到的各个音级仍然在调式音阶中。
对于音级 $C,E,G$ 做升高四个半音的严格移调，得到 $E,\sharp G,B$
如果这三个音级 $C,E,B$ 属于 $C$ 大调音阶，对其做相应的调性移调，得到的结果应为 $E,G,B$ 。
如果这三个音级属于 $F$ 大调音阶，对其做相应的调性移调，得到的结果应为 $E,G \flat B$ 。
将五线谱看作坐标系，横轴代表时间，纵轴代表音高，移调变换相当于沿着纵轴方向对旋律进行平移。
按照横轴方向对旋律进行变换，改变其时间顺序，关于某条垂线作旋律线的对称，称为逆行。
利用莫比乌斯带，在第一声部正向演奏时，第二声部逆向演奏，形成完整乐曲。
关于水平方向旋律对称，称为倒影。
选取不同水平直线作对称轴，得到不同的倒影。
勃拉姆斯第一交响曲的第三乐章主题就应用了倒影，并且计算相邻音级相差的倒影数后发现其为严格倒影，即保持音程的度数和性质不变，并且完全保留原旋律的节奏。
移调、逆行、倒影都可以看成是对一段旋律做的某种对称变换，而对称是美的重要来源。
传统音乐大多属于调性音乐，其中不同音级地位和作用不同，且总有一个主音，其他音与主音之间形成一定关系，这种关系限制了严格移调和倒影变换。
不过，这种情况到20世纪发生了很大变化，例如巴托克《小宇宙》和安东韦伯恩的一些作品。
贝多芬的作品，是古典主义和浪漫主义的交汇，其去世后古典主义差不多就灭绝了。
波兰作曲家肖邦，在 $e$ 小调前奏曲中采用半音化。
他力求从大小调调性体系中解放出来，最初运用了以全音阶为基础的"中立调性"，同时消除同音异名的区别，提倡同时采用或混用两种调性，从而使调性的解释放宽了，也致力于利用一切可用的声音源泉。
印象主义的技巧特点是忽视过去认为是结构性的因素，重视乐器的色彩变幻和和声的新颖刺激，印象主义的和声是浪漫主义主调音乐解体的最后阶段。
奥地利作曲家勋伯格在其音乐创作中逐步建立和发展了十二音技术，是作曲家有意识地采用数学变换（群论）的思想进行音乐创作的探索实践。

从乐音体系到音类空间

假设乐音体系由八个八度和 $C_8$ 构成， $M={C_0,\ldots,B_0,C_1,\ldots,B_7,C_8}$
可以把这 $97$ 个音级跟 $0 \sim 96$ 对应，例如 $48$ 代表中央 $C$ 。
根据这个对应，给定整数 $n \in Z$ ，将升高 $n$ 个半音的移调变换记作 $T_n$ ，则 $T_n(x)=x+n$
注意降低的移调变换和恒等变换。
数学上一个变换是某个集合到自身的映射，移调变换是乐音体系到自身的映射，因此变换后的结果仍然应该是一个音级。
但是，乐音按照八度关系循环，即进行同余意义下加法。
二元关系和有序对/笛卡尔积、等价关系、等价类的概念与性质，见《离散数学》课程。
协和音程具有自反性、对称性，但不满足传递性。
设 $M$ 是乐音体系的集合，称其中的两个音级具有八度关系，当且仅当其相等或者相差若干个八度，八度关系是 $M$ 上的一个等价关系。
给定一个等价关系，就得到集合中全部元素的一个分类。
乐音体系中根据八度关系形成的等价类称为音类，按照十二平均律，八度关系将所有的音级分成12个音类，如下

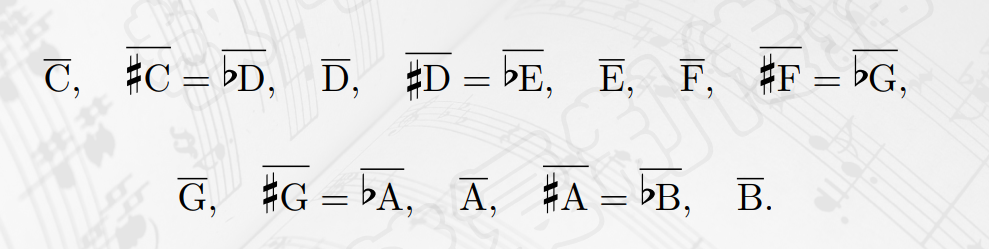
把12个音类放在一起，构成一个集合，称为音类空间。

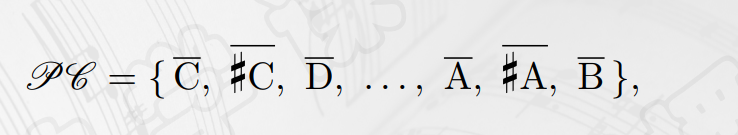
数学上，可以视为模12同余意义下的关系，接着对应模12同余类的并集合。
音类圆周，即音类把直线上的音级变成圆。
因此，音类空间可以与 $Z_{12}$ 一一对应。

音乐变换群

于是，可以给出移调变换的严格定义，也就是模 $12$ 意义下 $T_{n}(x)=x+n$
音类的这种数字表达式更容易计算。
易知，$T_{7}$ 与 $T_{-5}$ 意义相同。
即本质上只有12个移调变换。
可以看作变换的复合， $T_i * T_j$ 表示先进行 $T_j$ 再进行 $T_i$ ，注意与《离散数学》中的区别。
变换的复合在移调变换之间定义了一个运算，形成了一个代数结构。
它满足结合律，有单位元，且有逆元（对移调运算而言）。
那么，它是一个群，将群中运算称为乘法，将 $a$ 的逆元称为 $a^{-1}$ ，包含元素个数称为这个群的阶。
若满足交换律，则称为交换群或者 $Abel$ 群。
循环群，将 $T_1$ 记为生成元，由一个元素生成的元称为循环群。
例如，移调变换就是一个 $12$ 阶的循环群。
同时有，移调变换群与模 $12$ 加法群是同构的。
用符号 $I$ 表示中央 $C$ 不变的倒影变换。
可以得出倒影变换的计算公式 $I(x)=-x$ 在模 $12$ 的意义下。
复合变换 $T * I$ ，可以得到 $T*I(x)=1-x$ ，由 $T^{k} * I(x)=I * T^{-k}(x)$
可以将倒影变换与12个移调变换得到12个不同的变换，可以得出包含12个移调和12个倒影的更大的群。
则移调变换群是这个大群的子群。
正四边形的二面体群，可以得到顺时针旋转的 $r_{0},r_{90},r_{180},r_{270}$ 和关于对称轴/两条对角线的四个反射。
将它们合成一个群，称为二面体群，记作 $D_8$ 。
则上述更大群同构于正12边形的变换群，即 $D_{24}$
不过， $D_{2n},n \geq 3$ 不是交换群。
亦可以用置换和轮换表达式表示，具体见《离散数学》课程。
逆行变换： $R(x_1,x_2,\ldots,x_k)=x_k,x_{k-1},\ldots,x_1$
将逆行变换添进更大群，得到一个再大的群，称为音乐变换群。可以证明这个群的阶为48，其结构是一个直积。
即其同构于 $D_{24} \times Z_{2}$
其中元素形如， $T^{i},T^{i} * I,T^{i} * R,T^{i} * I * R$
群论的概念始于伽罗瓦，后续柯西、凯莱等人的论文再提出，十九世纪五十年代之前的音乐家不会知道群论。
李斯特的《匈牙利狂想曲第二号》就应用了群论的技巧。

十二音技术

十二音技术的出发点是十二音序列，一个音列是这12个音类的一个排列。
例如勋伯格的钢琴协奏曲，其基本音列为 $\flat E,\flat B,D,F,E,C, \sharp F,\flat A,\flat D,A,B,G$
以音列中第一个音类为起点，令其对应于 $0$ ，则其可以表示为 $Z_{12}$ 的一个排列，上述音列可以写为 $0,7,11,2,1,9,3,5,10,6,8,4$
给定一个音列，对其进行各种变换可以得到一系列新的音列。
作为出发点的音列称为初始音列，记作 $P_0$ ，例如对其进行移调变换，上升 $n$ 个半音得到的为 $P_n$ 。
共有12个移调音列，即 $P_0,P_1,\ldots,P_{11}$ 。
对 $P_n$ 作关于其第一个音类的倒影变换，得到一个倒影音列，记作 $I_n$ 。
对 $P_n$ 作逆行变换，得到一个逆行音列 $R_n$ 。
对 $I_n$ 作逆行变换，就得到逆行倒影音列 $RI_n$ 。
从初始音列 $P_0$ 出发，通过移调、倒影和逆行倒影变换，可以得到 $48$ 个音列，它们组成一个音列矩阵，是 $12 \times 12$ 的方阵。

音列中元素代表的是音类，在乐曲中具体使用哪个八度音符是由作曲家自己决定的。
可以在勋伯格《钢琴组曲》，罗忠镕《涉江采芙蓉》等见到。
但是，由于音列有对称性，从一个初始音列出发可以得到48个音列，但是其中可能有相等的。
例如 $P_0$ 是如下所示的全半音音阶，则只能得到24个互异的音列。

变换产生子集合，记 $|\Omega|$ 为全体音列组成的集合。
设 $\Omega$ 是一个有限集合， $G$ 是由 $\Omega$ 到自身的若干可逆变换构成的群， $\forall \alpha \in \Omega,$ 定义 $\Omega$ 的子集合 $Orb(\alpha)=\{\beta \in \Omega | \exists g \in G, G(\alpha)=\beta \}$
称为群 $G$ 的包含 $\alpha$ 的轨道。
从某个初始音列出发得到的48个音列就是音乐变换群的包含 $P_0$ 的轨道。
若存在 $g \not ={h} \in G$ ，使得 $g(P_0)=h(P_0)$ 则有 $h^{-1} * g(P_0)=P_0$ ，且 $h^{-1} * g \not ={e}$ ，即存在群中非恒等变换，保持 $P_0$ 不动。
对于 $\alpha \in \Omega$ ，记群 $G$ 的子集合 $G_{\alpha}=\{g \in G| g(\alpha)=\alpha \}$ ，称为 $\alpha$ 的稳定化子，它是一个子群。
轨道长度和稳定化子的阶之间有以下关系， $|Orb(\alpha)|=\frac{|G|}{|G_{\alpha}|}$
而 $|G|=48$ ，因此只需考虑 $|G_{\alpha}|$
定理：给定 $P_0=0,a_1,a_2,\ldots,a_{11}$ ，存在 $k,1 \leq k \leq 11,I_k=R_0$ 的充要条件为 $a_{11}+0 \equiv a_1+a_{10} \equiv \ldots a_{5}+a_{6} (\mathrm{mod} \ 12),k$ 为奇数。
满足这个定理的音列有 $(12)!! \times 6=276480$ 个，也不多。
勋伯格《小夜曲》第五乐章就满足上述定理。
定理：给定 $P_0=0,a_1,a_2,\ldots,a_{11}$ ，存在 $k,1 \leq k \leq 11,P_0=R_k$ 的充要条件是 $k=6,a_{6} \equiv a_5+6,a_7 \equiv a_4+6, \ldots, a_{11} \equiv 6 (\mathrm{mod} \ 12)$
满足这个定理的音列共有 $(12)!!=46080$ 个。
韦伯恩《交响曲》满足这个定理。
因此，可以得出，具有对称性的音列只占全部音列的 $\frac{1}{1485}$ ，非常稀少。
现代音乐具有一些社会功能，例如勋伯格的音乐，让人和音乐结合在一起。