数学的节奏与节奏的数学

时值序列

《为四件乐器而作》中，初始的时值序列为 $1,4,3,2$ 。
用增值变换相继产生新的时值序列 $4,16,12,8 / 3,12,9,6 / 2,8,6,4$
增值的倍数恰好等于时值序列本身 $1,4,3,2$
勋伯格的十二音技术是对音列作移调、倒影、逆行以及逆行倒影变换形成的。
后人发展其思想，进一步把音列与时值序列、力度、音区、音色等序列化的元素有机结合，形成整体序列主义。

计算时值序列

任意选定一个音类作为零点，给每个音列中的第 $i$ 项赋予一个数 $d_i$ ，它的值等于第 $i$ 项与零点之间相差的半音数。
例如，取 $F$ 作为零点，初始音列为 $0,1,4,9,5,8,3,10,2,11,6,7$
它们对应的 $d_i$ 分别为 $0,1,4,9,5,8,3,10,2,11,6,7$
移调音列和倒影音列都可以相应求出。
对于每个音列，按照上述方法都可以求出一个相应的时值序列 $(d_0,d_1,\ldots,d_{11}),0 \leq d_i \leq 11$
假定以十六分音符为时值单位 $1$ ，则有如下对应

再用初始音列 $P_0$ 加上时值序列，得到一段旋律。
例如，《为十二件乐器而作》第一乐章中，12间乐器平行地演奏各自的音列，一共4次。
表中出现的48个音列具有极强的规律性，共有6个移调音列和6个倒影音列，每个音列在表中恰出现两次，每次都有相应的逆行音列 $R_i$ 和 $RI_{j}$ 与其成对出现。

Clapping Music

相移：即正弦曲线的相位差，例如对 $y=sin \ x$ ， $y=sin(x+\frac{\pi}{6})$ 是其一个相移。
通过循环左移，造成。
假设恰有4拍休止符，且休止符不能连续出现，那么有多少种可能的节奏型？
考虑分配第一拍是不是休止符的情况，共 $C_{8}^{4}+C_{7}^{3}=105$ 种。
但是其中可能有相同的，因此考虑项链计数。
旋转等价：定义上述105个项链构成一个集合，定义其上变换，对于任意一条项链， $\sigma$ 表示把 $X$ 按照逆时针方向旋转30度，它是一个12阶的循环群。
可以定义一个等价关系，即两条项链可以通过旋转若干个30度达到相等。
对于群中的元素 $g \in G$ ，记 $g$ 的不动点集合为 $fix(g)={\alpha \in \Omega | g(\alpha)= \alpha }$
Burnside引理：设 $G$ 是集合 $\Omega$ 上的一个置换群，共有 $t$ 条轨道，则有 $t=\frac{1}{|G|}\sum_{g \in G}|fix(g)|$
群作用的两个定理，即从不动点集合出发求轨道数，或从稳定化子出发求轨道长度。
可以使用置换的轮换分解表示，该部分详见《离散数学》课程。
需要保持8颗绿色珠子在的位置整体不变，同时4颗红色珠子整体不变。
因此，$\sigma,\sigma^{11},\sigma^{2},\sigma^{10},\sigma^{4},\sigma^{8}$ 都没有不动点。
同时， $\e$ 有105个不动点， $\sigma^3$ 和 $\sigma^{9}$ 有3个不动点。
而， $\sigma^6$ 有9个不动点。
因此 $t=10$ 个轨道，可以对应以下节奏型。

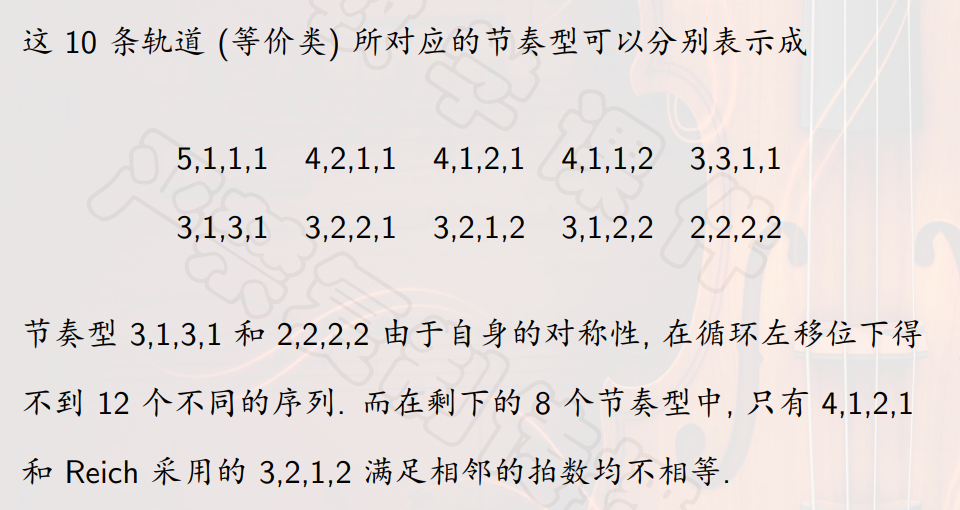
序列主义 VS 简约主义

Reich的音乐风格属于简约主义。
简约主义：采用简单的和声语言重复短小的音乐动机，使用最少的音乐材料达到尽可能大的效果。
音乐是时间的艺术，一段旋律转瞬即逝，需要反复呈现、不断强调，以给听众留下深刻印象。
因此，重复原则成为音乐发展的一项特殊的美学原则。
有音乐家认为，一系列事件需要有足够的内在冗余对抗由于注意力不集中等而产生的错误。
由此看来，实验音乐往往是一套有待研究的关系，而非有待聆听的音乐，音乐几乎无法从听觉上进行核查和矫正。
为间歇性聆听创作音乐的方法应该是提供足够的冗余，这是越来越多的当代作曲家，例如简约主义者在做的事情。
他们写作的音乐不仅具有冗余性，而且其冗余性持续不断，甚至富有侵略性。
从历史发展的角度来看，音乐本身就是一个不断发展、不断更新的过程，成熟的艺术恰恰是建立在必然到自由的基础上的。
有两种音乐家，一种是发明语言的，一种是打包语言的。
例如《镜中镜》跟《指环王2》中的插曲，就体现了这一点，后者还利用了泛三和弦。

数学和音乐

由于数和形都是抽象的产物，因此数学是抽象的。
数学不是自然科学，因为科学理论必须是能够被证伪的。
音乐也有抽象性，音高的概念是连续频谱中的离散点，也是抽象的产物。
音乐是抽象的艺术，不具备造型性和语义性。
造型性是可见的，具有空间占位，相对固定。
音乐要把内在的东西表达出来，但是在这种客观存在中仍然是主体性的。
对于语义性，语义是单词、短语、符号、图形等代表的含义。
数学是高度形式化的，它研究经过抽象的、抽取掉了具体内容的形式。
音乐也是形式化的，所有艺术都追求形式和内容的统一，而只有音乐实现了完美结合，音乐的内容就是乐音的运动形式。
数学跟音乐都有独特的符号系统。
它们都有不同的内在逻辑跟发展路径。