一维振动方程

乐器的分类

• 气鸣乐器：边棱、唇鸣、簧鸣等。
• 弦鸣乐器：弓拨、弹拨、击打等。
• 电鸣乐器。
• 体鸣乐器：打击乐、木琴。
• 膜鸣乐器：鼓、卡祖笛等。
• 一维上我们只考虑弦鸣乐器。

抽象化

• 一个假设：均匀细弦。
• 三个参数：长度$L$，受到张力$T$，单位长度的质量/弦密度$\rho$，用于衡量弦粗细。

数学建模

• 一条水平弦被固定在水平轴$(0,0)$和$(L,0)$之间，设$u(x,t)$为位置$x$在时刻$t$时的位移。取弦上的一小段$\overline{PQ}$,其中$P=(x_0,u(x_0,t)),Q=(x_0+\Delta x,u(x_0+\Delta x,t))$.

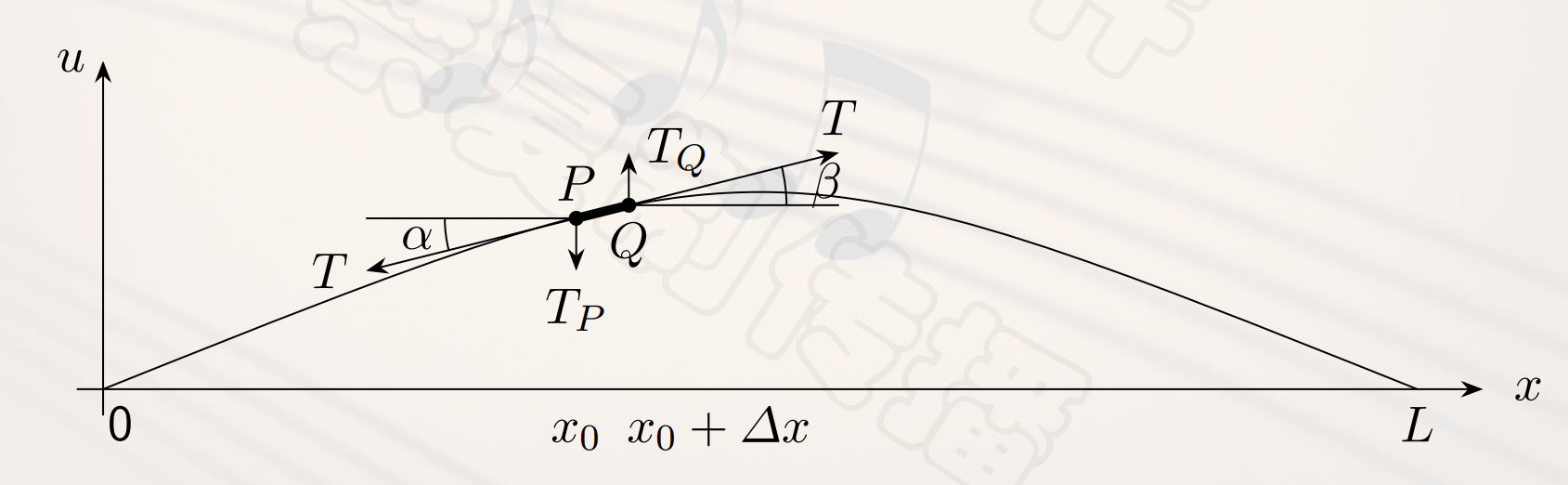
• 运用牛顿第二定律，$PQ$受到的力$F=T_Q-T_P \approx T(\tan \beta - \tan \alpha)$，质量$m=\rho \Delta x$.
• 由牛顿第二定律得到，$T(\frac{\partial u}{\partial x} \mid_{x=x_0+\Delta x}-\frac{\partial u}{\partial x} \mid_{x=x_0})=\rho \Delta x \cdot a$.
• 化简得到$\frac{(\frac{\partial u}{\partial x} \mid_{x=x_0+\Delta x}-\frac{\partial u}{\partial x} \mid_{x=x_0})}{\Delta x}=\frac{\rho}{T} \cdot a$.
• 令$\Delta x \to 0$，得到$\frac{\partial^2 u}{\partial x^2}=\frac{\rho}{T}\frac{\partial^2 u}{\partial T^2}|_{x=x_0}$.
• 由于$x$的任意性，得到$\frac{\partial^2 u}{\partial x^2}=\frac{\rho}{T}\frac{\partial^2 u}{\partial t^2}$.
• 再令$c=\sqrt{\frac{T}{\rho}}$，得到均匀细弦上的位移函数$u(x,t)$需满足的一维振动方程：$\frac{\partial^2 u}{\partial t^2}=c^2\frac{\partial^2 u}{\partial x^2}$
• 由于弦的两边是固定的，所以上述一维振动方程还需要满足边值条件：$u(0,t)=u(L,t)=0,\forall t \geq 0$.
• 使用分离变量法解上述方程。
• 得到方程的解$u(x,t)=\sum\limits_{n=1}^{+\infty}(a_n \cos \frac{n \pi c}{L}t+b_n \sin \frac{n \pi c}{L}t) \sin (\frac{n \pi}{L}x)$.
• 对于每个$u_n(x,t)$，它是两部分的乘积，前一部分是时间的函数，后一部分是位置的函数，令$w_n=\frac{n \pi c}{L}, \tan \theta_n=\frac{a_n}{b_n},$得到$u(x,t)=\sqrt{a_n^2+b_n^2} \sin (w_nt+\theta_n) \sin \frac{n \pi}{L}x$.

振动模态与泛音

振动模态

• 弦的振动是无穷多个正弦振动的叠加。
• 对于$u(x,t)=\sqrt{a_n^2+b_n^2} \sin (w_nt+\theta_n) \sin \frac{n \pi}{L}x$，称为弦振动的第$n$个振动模态。
• 在弦中间任意固定一点$x_0$，则可以得到$x_0$的第$n$个振动模态。
• $\mathrm{Mersenne}$定律：$x_0$的第$n$个振动模态频率为$f_n=\frac{n}{2L}\sqrt{\frac{T}{\rho}}$，$n=1$时，$f_1=\frac{1}{2L}\sqrt{\frac{T}{\rho}}$.

泛音

• 弦的振动频率组成的序列$f_1,f_2,\ldots$称为弦的固有频率。
• 基频：$f_1$，相应的声音称为基音。
• 泛音：$f_n(n>1)$对应的声音，通常称$f_2$对应第一泛音，$f_3$对应第二泛音等等。
• 由上述公式可知，所有泛音的频率都是基频整数倍。
• 泛音列：$f,2f,3f,\ldots$。
• 波节：振幅为0，即点$x=\frac{kL}{n}$处，即高中物理中的波峰波谷。
• 波腹：振幅最大，即点$x=\frac{kL}{2n}$处，即高中物理中的平衡位置。

协和音程泛音列重合理论

• 由赫尔姆霍兹发现，一个音列与泛音列的重合度越高，那么这个音听起来越和谐。
• 例如八度音程$2f,4f,\ldots$有一半的音与泛音列重合，听起来非常和谐。
• 纯五度音程$\frac{3}{2}f,3f,\frac{9}{2}f,\ldots$有一部分音与泛音列重合，听起来比较和谐。
• 大二度音程$\frac{9}{8}f,\frac{9}{4}f,\frac{27}{8}f$，没有任何音与泛音列重合，听起来不和谐。

泛音与小号

• 自然小号/巴洛克小号：长度为现代小号的两倍，声音比现代小号低一个八度。号管上没有开孔和活塞按键，只能发出基频的自然泛音。
• C调自然小号的基音是$C_2$，第一泛音为$C_3$，通常演奏者从第二泛音($G_3$)开始。
• 由于小三度的比例为$6:5=1.2$，得出4倍基频的为$C_4$，5倍基频的为$E_4$，6倍基频的为$G_4$，又由于$7:6 \approx 1.16$，7倍基频为$\flat B_4$，八倍基频的为$C_5$。
• 大二度的比例为$9:8=1.125$，所以9倍基频为$D_5$，10倍基频为$E_5$，由于$11:9 \approx 1.2$，11倍基频为$F_5$，$12:10=1.2$，12倍基频为$G_5$，由于$13:12 \approx 1.08$，13倍基频为$A_6$。

泛音与古琴

• 泛音演奏：古琴曲《流水》，《沧海一声笑》。
• 古琴音色按照弹法可以分为三类：
  • 泛音：象征天，有清冷入仙感，轻盈活泼。
  • 散音：象征地，松陈旷远，深沉浑厚。
  • 按音：象征人，婉转抒情，缥缈多变。
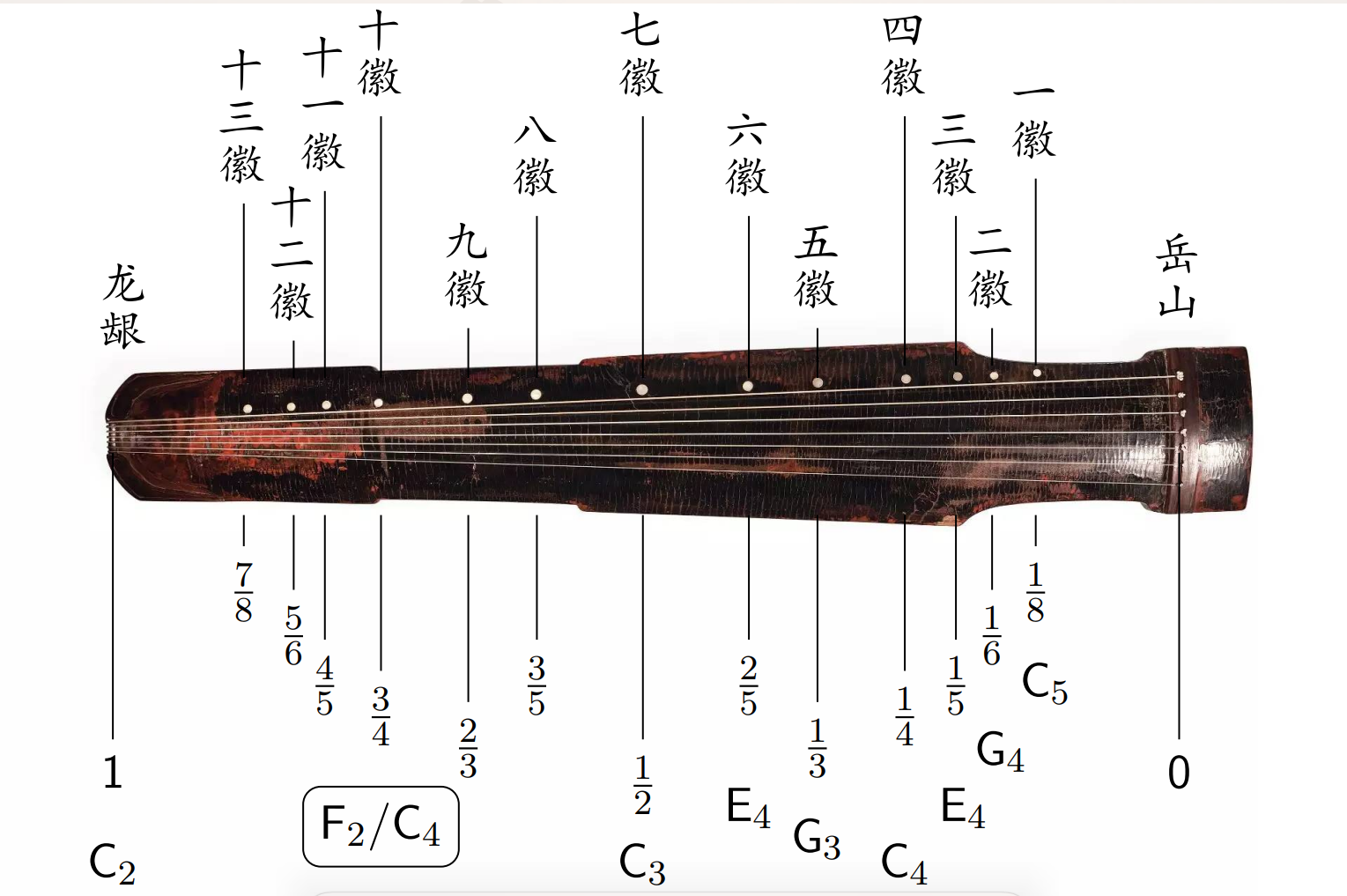
• 古琴的结构如下图所示，若按一下七徽则奇数倍基频被破坏，偶数倍基频不变。
• 得出结论，按一下，相乘能成为整数的基频倍数不被破坏。

泛音与呼麦

• 呼麦/喉音唱法/泛音唱法/多声唱法：演唱者运用口腔不同部位的气息控制，突出某些泛音，产生同时唱出两个声部的效果。
• 2009年，呼麦被列入联合国教科文组织非物质文化遗产代表名录。

拨弦与傅里叶级数

• 为确定$a_n,b_n$，需要以下方程：

$$\begin{cases} \frac{\partial^2 u}{\partial t^2}=c^2 \frac{\partial^2 u}{\partial x^2}, & x \in [0,L],t \geq 0 \\ u(0,t)=u(L,t)=0, & \forall t \geq 0 , \quad (边值条件) \\ u(x,0)=\phi(x), & \forall x \in [0,L] , \quad (初始形状) \\ \frac{\partial u}{\partial t}_{t=0}=\psi(x), & \forall x \in [0,L] , \quad (初始速度) \\ \end{cases}$$

• 本课程主要介绍特殊情况，即拨弦。
• 给定$x_0 \in (0,L)$和常数$h>0$，假设把弦上$x_0$点拨到距离原来位置$h$的的地方，则此时的$\phi(x)$是折线函数，方程为$\phi(x)=\begin{cases}\frac{hx}{x_0}, \quad 0 \leq x \leq x_0, \\ \frac{h(x-L)}{x_0-L}, \quad x_0 \leq x \leq L \end{cases}$.
• 将$t=0$代入，得$\phi(x)=u(x,0)=\sum\limits_{n=1}^{+\infty}a_n \sin (\frac{n \pi}{L}x)$.
• 有关傅里叶级数的介绍，详见《高等数学A（下）》课程。
• 将$\phi(x)$奇延拓到$[-L,0]$，再进行周期延拓，得到$a_n=\frac{1}{L}\int_{-L}^{L}\phi(x) \sin \frac{n \pi}{L}xdx$.
• $\psi(x)$也被表示为一个傅里叶级数，$\psi(x)=\sum\limits_{n=1}^{+\infty}b_n \frac{n \pi c}{L} \sin (\frac{n \pi}{L}x)$。
• 同理可以求出$b_n=\frac{1}{L}\int_{-L}^{L}\psi(x) \sin \frac{n \pi}{L}xdx$.
• 假设在拨弦的手指放开时弦是静止的，即弦上任一点的的初速度为$0$，$\psi(x)=0,\forall x \in [0,L],$则所有的系数$b_n=0$。
• 得到最终结果，给定长度为$L$，两端均固定的弦，在其中点$\frac{L}{2}$处拨动，假定释放时弦上各处的初速度均为0，则弦产生的振动为$u(x,t)=\sum\limits_{n=1}^{+\infty}(a_n \cos \frac{n \pi c}{L}t+b_n \sin \frac{n \pi c}{L}t) \sin (\frac{n \pi}{L}x)=\sum\limits_{k=0}^{+\infty}\frac{8}{(2k+1)^2 \pi^2} \cos (\frac{(2k+1) \pi c}{L}t) \sin (\frac{(2k+1) \pi}{L}x)$.
• 拨弦的各振动模态的频率都是基频的奇数倍，在弦振动的固有频率中，只有对应于奇数的频率才会出现。
• 几何解释：在$\frac{L}{2}$释放弦后，弦的振动应当始终保持关于其对称，$n$为奇数时是对称的，而偶数时的波形是反对称的。
• 吉他上的品与泛音息息相关，十二品处于中间位置。

空穴来风

管乐器

• 管乐器通常分为两组：
  • 木管组：短笛、长笛、双簧管、单簧管、大管等。
  • 铜管组：小号、圆号、长号、大号等。
• 木管五重奏通常由长笛、双簧管、单簧管、大管和圆号组成。
• 管乐器的振动主体是管内的空气柱，但边值条件与弦振动的不同。振动的空气柱会超出管的端口，需要对其音高/频率进行端口校正。最早由明朝朱载堉提出。
• 声音是纵波，管子中的空气柱振动时，沿着管子的轴向方向形成疏密相间的拨动。
• 不考虑管口校正的情况下，在开口处，空气柱可以自由移动，振动幅度最大，形成波腹。
• 如果管子的一端是封闭的，则该处的空气柱无法做纵向的振动，形成波节。
• 从波腹到波节刚好构成一个完整振动周期的$\frac{1}{4}$，即距离恰等于$\frac{1}{4}$波长。

开管的振动模态

• 不计管口校正，开口位置总是位于振动的波腹，闭口位置只能位于波节。
• 对于基频，有$L=\frac{\lambda_1}{2}$，对于$f_n$，有$L=\frac{n\lambda_n}{2}$。
• 即开管的泛音列为$f,2f,3f,\ldots$。

闭管的振动模态

• 不计管口校正，开口位置总是位于振动的波腹，闭口位置只能位于波节。
• 对于基频，有$L=\frac{\lambda_1}{4}$，对于$f_n$，有$L=\frac{(2n-1)\lambda_n}{4}$。
• 即闭管的泛音列为$f,3f,5f,\ldots$，即闭管只有偶次泛音。

管乐器实例

• 长笛是一种开管，单簧管是一种闭管。
• 假设有效管长$L \approx 0.66m,$声速$v=340m/s$。
• 对于长笛，其基频$f_1=\frac{v}{\lambda_1}=\frac{v}{2L}=\frac{340}{1.32}=258 \mathrm{Hz}$。
• 对于单簧管，其基频$f_1=\frac{v}{\lambda_1}=\frac{v}{4L}=\frac{340}{2.64}=129 \mathrm{Hz}$。
• 普通长笛的最低音为$C_4$（中央$C$），普通的$\flat B$单簧管的最低音为$D_3$，记谱为$E_3 -$移调乐器。
• 长笛的泛音列中，第二项的频率为$2f$，超吹产生高八度的音。
• 单簧管的泛音列中，第二项的频率为$3f$，超吹产生高十二度的音。

思考题

• 乐音和噪音的本质区别是什么？
• 发出乐音的声源的振动是规则的，而发出噪音的声源的振动是不规则的。乐音是由一系列频率整数倍关系的正弦波叠加而成的，而噪音则是由频率分布较为均匀的波叠加而成的。
• 为什么单簧管只能发出偶次泛音，而自然小号可以发出所有的泛音？
• 因为单簧管是一种闭管，而自然小号是一种开管。

声明

本笔记的部分内容来自喵喵的学习笔记 ，如有侵权请联系我删除。